Life-cycle cost (or impact) model

In this section, a new model is proposed by modifying traditional Morkovian deterioration models to account for the changing deterioration rates. This study is specifically motivated by the emergence of new intervention options, such as FRP strengthening, where once strengthened the critical deterioration mechanism may be changed from that of the pre-strengthened element.

For example, a possible intervention for a RC beam is to be strengthened using externally bonded FRP laminates. After such an intervention, the critical deterioration mechanism (in terms of the strength reduction) of the strengthened beam becomes the interfacial damage of the FRP-concrete interface [11-12], which will have a different deterioration rate (typically slower) than that of the original RC beam.

The model developed in this study takes into consideration the following possibilities:

1. Certain interventions may improve the condition of the element without changing the deterioration rate/mechanism (e.g. paint restoration of a painted steel girder).
2. Certain types of interventions may improve the condition of the element and also change the deterioration rate/ mechanism (e.g. FRP strengthening of RC girders).
3. Interventions possible in an intermediate state of deterioration may not be possible if structural failure occurs (e.g. a deteriorating RC beam may be strengthened using FRP strengthening. However, if the beam has experienced structural failure, replacement may be the only viable option). Therefore, it is important to distinguish between the failure CS (typically considered as the worst CS in current practice) and structural failure. Structural failure of an element may occur at any stage irrespective of the CS of the element.
4. Interventions such as FRP strengthening are aimed predominantly at existing structures. Advantages of FRP strengthening over conventional strengthening methods, e.g. low labor costs, minimal disturbance to the traffic etc., may not have the same significance when used in new structural elements. Therefore, if structural failure occurs in an element (un-strengthened or strengthened), it may or may not be replaced by a new strengthened element. More likely, it will be replaced by a new un-strengthened element.

In the following sections, first a condition-based transition probability matrix considering the structural failure of an element is presented. Secondly, a method to model interventions that will not change the original deterioration rate (explicitly accounting for structural failure)based on steady state Markovian probabilities is presented. Finally, a model is proposed to account for interventions that will result in a change in the deterioration rate.

Condition based transition probability matrix for deterioration modeling

Transition probabilities represent the probability for an element that is in CS i at time period t to be in state j at the following time period (i.e. t+1). A typical transition probability matrix of an element with n CSs can be written as:

$P_e=p_{ij}^e=\left[\begin{array}{cccc}{p}_{11}^e& p_{12}^e& \cdots & p_{1n}^e\\ 0& p_{22}^e& \cdots & p_{2n}^e\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right]\text{ (1)}$

with:

$$\left\{\begin{array}{c}{\displaystyle \sum _{j=1}^n{p}_{ij}^e=1\forall i,j}\\ p_{ij}^e=0\text{ when }(i>j)\end{array}\right.\text{ (2)}$$

Where index e denotes the element of concern, and n is the number of CSs for element e. An appropriate (stochastic) deterioration model can be used to estimate the transition probabilities in absence of inspection data.

In such a transition matrix the worst (i.e. highest) CS is defined as the CS where the element performance becomes inadequate. However, the probability that the element may experience structural failure within a time interval is not explicitly considered. The probability of the element structural failure is dependent on the current CS of the element. In the current study, a new CS, i.e. CSn+1, is introduced to accommodate the structural failure of the element. The structural failure considered in this study is the result of the applied load exceeding the structural resistance, thus causing a sudden change in the structure condition. Therefore it is assumed that, if the structural failure didn’t occur, deterioration (e.g. corrosion) would continue to follow the normal path as predicted by the stochastic deterioration model. With this assumption, a new transition probability matrix can be written, considering the annual structural failure probability of the element, as:

$${\overline{P}}_e=\left[\begin{array}{ccccc}{\overline{p}}_{11}^e& {\overline{p}}_{12}^e& \cdots & {\overline{p}}_{1n}^e& {\overline{p}}_{1n+1}^e\\ 0& {\overline{p}}_{22}^e& \cdots & {\overline{p}}_{2n}^e& {\overline{p}}_{2n+1}^e\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 1-{\overline{p}}_{nn+1}^e& {\overline{p}}_{nn+1}^e\end{array}\right]\text{ (3)}$$

Where

$$\left\{\begin{array}{l}{\overline{p}}_{ij}^e=\left(1-F_i^e\right)p_{ij}^e\forall j<n+1\\ {\displaystyle \sum _{j=1}^n{\overline{p}}_{ij}^e=1-F_i^e\forall i,j}\\ {\overline{p}}_{in+1}^e=F_i^e\\ {\overline{p}}_{ij}^e=0\text{ when }(i>j)\end{array}\right.\text{ (4)}$$

Where F^e_i is the structural failure probability of an element in CS i.

Case 1: When the interventions result in elements with properties that are similar to the original elements

In typical Markovian models, interventions are assumed to improve the condition of the elements, but assumed not to change the deterioration rate. Therefore, deterioration matrix remains the same after the interventions. If the element undergoes structural failure, and is replaced by an element similar to the original, then again the deterioration rate can be assumed to remain unchanged.

The effectiveness matrix of the intervention carried out at CSs 1, 2, …, n+1can be defined using the transition probabilities representing the probability for an element that is in CS i at the time of intervention to be in state j after the interventions set x as:

$R_e\left(x,i^{\text{'}}\right)=r_{ij}^{e,x}=\left[\begin{array}{cccc}{r}_{1,1}^{e,x}& r_{1,2}^{e,x}& \cdots & r_{1,n}^{e,x}\\ r_{2,1}^{e,x}& r_{2,2}^{e,x}& \cdots & r_{2,n}^{e,x}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n+1,1}^{e,x}& r_{n+1,2}^{e,x}& \cdots & r_{n+1,n}^{e,x}\end{array}\right]\text{ (5)}$

With the properties:

$$\left\{\begin{array}{l}{r}_{ij}^{e,x}\ge 0\forall i,j\\ {\displaystyle \sum _{j=1}^n{r}_{ij}^{e,x}=1\forall i=i^{\text{'}}}\\ {\displaystyle \sum _{j=1}^n{r}_{ij}^{e,x}=0\forall i\ne i^{\text{'}}}\end{array}\right.\text{ (6)}$$

Where ' i denotes the CSs where interventions will be carried out. Note that this is an n+1 by n matrix, as any intervention carried out on the element will improve the condition, thus the probability of structural failure is assumed to be negligible immediately after the intervention. Also, it is reasonable to assume that the interventions on any of the CSs i’=1, 2, ...,n (i.e. non-structural failure CSs) will be carried out only if the element does not experience structural failure prior to the intervention. If the element experience structural failure, it will be immediately replaced by a new element. Therefore the resulting deterioration-intervention matrix for a single time interval can be written as:

$${\overline{Q}}_e\left(x,i^{\text{'}}\right)={\overline{q}}_{ij}^e={\widehat{p}}_{ij}^e+\left[1-{\overline{p}}_{in+1}^e\right]r_{ij}^{e,x}+{\overline{p}}_{in+1}^e{r}_{n+1j}^{e,x}{{\displaystyle }}_{}i,j=1,2,\mathrm{...},n\text{ (7)}$$

Where

$$\left\{\begin{array}{l}{\widehat{p}}_{ij}^e={\overline{p}}_{ij}^e\forall i\ne i^{\text{'}}\\ {\widehat{p}}_{ij}^e=0\underset{}{}\forall i=i^{\text{'}}\end{array}\right.\text{ (8)}$$

The CS of the element in any given year can be obtained by multiplying the CS of the element at the beginning of each year by deterioration-intervention matrix, ( ) ' Q x,i e , i.e.:

$${\Pi }_e\left(t,x,i^{\text{'}}\right)={\Pi }_e\left(0\right){\left({\overline{Q}}_e^{}\left(x,i^i\right)\right)}^t\text{ (9)}$$

where

$${\Pi }_e\left(0\right)=\left\{\begin{array}{cccc}{\pi }_1^e\left(0\right)& {\pi }_2^e\left(0\right)& \cdots & {\pi }_n^e\left(0\right)\end{array}\right\}$$

is the CS distribution of the element at time t=0.

The expected total costs or impacts in any given year are the sum of intervention costs (in both structural failure and non-structural failure CSs) and costs incurred due to the normal operations of the bridge. Therefore, the expected cost or value of impacts in any given year can be written as:

$$\begin{array}{l}E\left(V_t\left(x,i^{\text{'}}\right)\right)={\displaystyle \sum _{\forall i=i^{\text{'}}}^{}{\displaystyle \sum _{j=1}^n{\pi }_j^e\left(t-1\right){\overline{p}}_{ji}^e{\displaystyle \sum _{a=1}^A{c}_{a,x}^{e,I}}}}\\ +{\displaystyle \sum _{j=1}^n{\pi }_j^e\left(t-1\right){\overline{p}}_{jn+1}^e}{\displaystyle \sum _{a=1}^A{c}_a^{e,f}}+{\displaystyle \sum _{j=1}^n{\pi }_j^e\left(t\right){\displaystyle \sum _{a=1}^A{c}_{a,j}^{e,D}}}\left(1-\frac{d_t\left(x,i^{\text{'}}\right)}{d_{T,t}}\right)\text{ (10)}\end{array}$$

where ( 1) π^e_j(t −1) is the probability of element being in CS j in time t-1, c ^e,I_a,xis the value of impact a in carrying out intervention x in non-structural failure CS ' i on element e, c ^e,f_ais the value of impact a in an event of the failure of element e, c^e,D _a,jis the value of impact a when the element is in operation and in CS j, d _{T ,t}is the length of the time interval t in days, and ' d_t (x,i) is the number of days per time interval t that the structure is out of service due to interventions x, which can be calculated as:

$d_t\left(x,i^{\text{'}}\right)={\displaystyle \sum _{\forall i=i^{\text{'}}}^{}{\displaystyle \sum _{j=1}^n{\pi }_j^e\left(t-1\right){\overline{p}}_{ji}^e{d}_x^{e,I}}}+{\displaystyle \sum _{j=1}^n{\pi }_j^e\left(t-1\right){\overline{p}}_{jn+1}^e}{d}_{n+1}^{e,f}\text{ (11)}$

Where d ^e,I_xis the number of days when the element will be out of service for interventions x carried out on non-structural failure CSs ' i , and d^e,f _n+1 is the number of days when the element will be out of service due to failure. The optimal intervention strategy, i.e. intervention set x, and CSs ' i where the interventions will be carried out can be written as:

$$\forall x\in X,i^{\text{'}}\in i,E\left(T{V}_t\left(x,i^{\text{'}}\right)\right)=\min \left[{\displaystyle \sum _{t=0}^{T}E\left(V_t\left(x,i^{\text{'}}\right)\right){\left(\frac{1}{1+r}\right)}^t}\right]\text{ (12)}$$

Case 2: When the interventions use elements with different properties from the original elements

When an intervention changes the deterioration rate, the above described modeling approach is no longer applicable. If the deterioration rate changes, a new deterioration matrix is needed to model for the post-intervention element. If such an intervention of the original element is carried out in CSi, we can assume that the element CS will transit to a new deterioration matrix, which has the transition probabilities corresponding to the new element (postintervention element) deterioration rate. In order to represent this in a transition probability matrix, the deterioration of the new element (denote by index 2) is modeled using k+1 CSs with CS k+1 representing the structural failure of the new element:

$${\overline{P}}_2=\left[\begin{array}{ccccc}{\overline{p}}_{11}^2& {\overline{p}}_{12}^2& \cdots & {\overline{p}}_{1k}^2& {\overline{p}}_{1k+1}^2\\ 0& {\overline{p}}_{22}^2& \cdots & {\overline{p}}_{2k}^2& {\overline{p}}_{2k+1}^2\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 1-{\overline{p}}_{kk+1}^2& {\overline{p}}_{kk+1}^2\end{array}\right]\text{ (13)}$$

The effectiveness vector of the interventions carried out at structural failure can be defined using the transition probabilities for an element in structural failure CS f(i.e. f=n+1, or f=k+1) at the time of interventions x, to be in state j after the intervention as:

${\widehat{R}}_f\left(x\right)={\widehat{r}}_{fj}^{e,x}=\left[\begin{array}{cccccccc}{\widehat{r}}_{f1}^{1,x}& {\widehat{r}}_{f2}^{1,x}& \cdots & {\widehat{r}}_{fn}^{1,x}& {\widehat{r}}_{f1}^{2,x}& {\widehat{r}}_{f2}^{2,x}& \cdots & {\widehat{r}}_{fk}^{2,x}\end{array}\right]\text{ (14)}$

With

$$\left\{\begin{array}{l}{\widehat{r}}_{fj}^{2,x}=0{{\displaystyle }}_{}\forall j{{\displaystyle }}_{}if{{\displaystyle }}_{}Int=1\\ {\widehat{r}}_{fj}^{1,x}=0{{\displaystyle }}_{}\forall j{{\displaystyle }}_{}if{{\displaystyle }}_{}Int=2\\ {\displaystyle \sum _{j=1}^n{\widehat{r}}_{fj}^{1,x}}+{\displaystyle \sum _{j=1}^k{\widehat{r}}_{fj}^{2,x}}=1\end{array}\right.\text{ (15)}$$

Where Int x ∈ denotes the element to be chosen to replace the failed element, i.e. if Int=1, element similar to original element (element 1) will be used, and if Int=2, then an element similar to the new element (element 2) will be used.

Similarly, it is assumed that an intervention carried out on element 1for CSs i=1,…,n, will have the option to use elements either similar to the original element (i.e. element 1) or those similar to element 2. The effectiveness matrix of the interventions for element 1 can be defined using the transition probabilities representing the probability for element 1 in CS i at the time of intervention to be in CS j (of element 1 or 2) after the intervention set x as:

$${\widehat{R}}_1\left(x,i^{\text{'}}\right)={\widehat{r}}_{ij}^{e,x}=\left[\begin{array}{cccccccc}{\widehat{r}}_{11}^{1,x}& {\widehat{r}}_{12}^{1,x}& \cdots & {\widehat{r}}_{1n}^{1,x}& {\widehat{r}}_{11}^{2,x}& {\widehat{r}}_{12}^{2,x}& \cdots & {\widehat{r}}_{1K}^{2,x}\\ {\widehat{r}}_{21}^{1,x}& {\widehat{r}}_{22}^{1,x}& \cdots & {\widehat{r}}_{2n}^{1,x}& {\widehat{r}}_{21}^{2,x}& {\widehat{r}}_{22}^{2,x}& \cdots & {\widehat{r}}_{2K}^{2,x}\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮\\ {\widehat{r}}_{n1}^{1,x}& {\widehat{r}}_{n2}^{1,x}& \cdots & {\widehat{r}}_{nn}^{1,x}& {\widehat{r}}_{n1}^{2,x}& {\widehat{r}}_{n2}^{2,x}& \cdots & {\widehat{r}}_{nK}^{2,x}\end{array}\right]\text{ (16)}$$

with

$$\left\{\begin{array}{l}{\widehat{r}}_{ij}^{2,x}=0{{\displaystyle }}_{}\forall i{{\displaystyle }}_{}if{{\displaystyle }}_{}Int=1\\ {\widehat{r}}_{ij}^{1,x}=0{{\displaystyle }}_{}\forall i{{\displaystyle }}_{}if{{\displaystyle }}_{}Int=2\\ {\displaystyle \sum _{j=1}^n{\widehat{r}}_{ij}^{1,x}}+{\displaystyle \sum _{j=1}^k{\widehat{r}}_{ij}^{2,x}}=1{{\displaystyle }}_{}\forall i=i\text{'}\\ {\widehat{r}}_{ij}^{2,x}={\widehat{r}}_{ij}^{2,x}=0{{\displaystyle }}_{}{{\displaystyle }}_{}{{\displaystyle }}_{}\forall i\ne i\text{'}\end{array}\right.\text{ (17)}$$

Similarly, the interventions on element 2 can be using the elements similar to element 1, or those similar to element 2. Therefore, the effectiveness matrix of the interventions for element 2 can be defined using the transition probabilities representing the probability for element 2 in CS i at the time of intervention to be in CS j (of element 1 or 2) after the intervention set x as:

$${\stackrel{⌣}{R}}_2\left(x,i^{\text{'}}\right)={\stackrel{⌣}{r}}_{ij}^{e,x}=\left[\begin{array}{cccccccc}{\stackrel{⌣}{r}}_{11}^{1,x}& {\stackrel{⌣}{r}}_{12}^{1,x}& \cdots & {\stackrel{⌣}{r}}_{1n}^{1,x}& {\stackrel{⌣}{r}}_{11}^{2,x}& {\stackrel{⌣}{r}}_{12}^{2,x}& \cdots & {\stackrel{⌣}{r}}_{1k}^{2,x}\\ {\stackrel{⌣}{r}}_{21}^{1,x}& {\stackrel{⌣}{r}}_{22}^{1,x}& \cdots & {\stackrel{⌣}{r}}_{2n}^{1,x}& {\stackrel{⌣}{r}}_{21}^{2,x}& {\stackrel{⌣}{r}}_{22}^{2,x}& \cdots & {\stackrel{⌣}{r}}_{2k}^{2,x}\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮\\ {\stackrel{⌣}{r}}_{k1}^{1,x}& {\stackrel{⌣}{r}}_{k2}^{1,x}& \cdots & {\stackrel{⌣}{r}}_{kn}^{1,x}& {\stackrel{⌣}{r}}_{n1}^{2,x}& {\stackrel{⌣}{r}}_{k2}^{2,x}& \cdots & {\stackrel{⌣}{r}}_{kk}^{2,x}\end{array}\right]\text{ (18)}$$

with

$$\left\{\begin{array}{l}{\stackrel{⌣}{r}}_{ij}^{2,x}=0{{\displaystyle }}_{}\forall i{{\displaystyle }}_{}if{{\displaystyle }}_{}Int=1\\ {\stackrel{⌣}{r}}_{ij}^{1,x}=0{{\displaystyle }}_{}\forall i{{\displaystyle }}_{}if{{\displaystyle }}_{}Int=2\\ {\displaystyle \sum _{j=1}^n{\stackrel{⌣}{r}}_{ij}^{1,x}}+{\displaystyle \sum _{j=1}^k{\stackrel{⌣}{r}}_{ij}^{2,x}}=1{{\displaystyle }}_{}\forall i=i\text{'}\\ {\stackrel{⌣}{r}}_{ij}^{2,x}={\stackrel{⌣}{r}}_{ij}^{2,x}=0{{\displaystyle }}_{}{{\displaystyle }}_{}{{\displaystyle }}_{}\forall i\ne i\text{'}\end{array}\right.\text{ (19)}$$

Effectiveness matrices for elements 1 and 2, considering interventions on non-structural failure CS will be carried out only if the elements didn’t fail, can be combined as: With:

$${\overline{R}}_c\left(x,i^{\text{'}}\right)={\overline{r}}_{ij}^{c,x}=\left[\begin{array}{cccccc}{\overline{r}}_{1,1}^{c,x}& \cdots & {\overline{r}}_{1,n}^{c,x}& {\overline{r}}_{1,n+1}^{c,x}& \cdots & {\overline{r}}_{1,n+k}^{c,x}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ {\overline{r}}_{n,1}^{c,x}& \cdots & {\overline{r}}_{n,n}^{c,x}& {\overline{r}}_{n,n+1}^{c,x}& \cdots & {\overline{r}}_{n,n+k}^{c,x}\\ {\overline{r}}_{n+1,1}^{c,x}& \cdots & {\overline{r}}_{n+1,n}^{c,x}& {\overline{r}}_{n+1,n+1}^{c,x}& \cdots & {\overline{r}}_{n+1,n+k}^{c,x}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ {\overline{r}}_{n+k,1}^{c,x}& \cdots & {\overline{r}}_{n+k,n}^{c,x}& {\overline{r}}_{n+k,n+1}^{c,x}& \cdots & {\overline{r}}_{n+k,n+k}^{c,x}\end{array}\right]\text{ (20)}$$

With:

$$\left\{\begin{array}{l}{\overline{r}}_{ij}^C=\left[1-{\overline{p}}_{in+1}^1\right]{\widehat{r}}_{ij}^e{{\displaystyle }}_{}\forall i\le n\\ {\overline{r}}_{ij}^C=\left[1-{\overline{p}}_{iK+1}^2\right]{\stackrel{⌣}{r}}_{ij}^e{{\displaystyle }}_{}\forall n+1\le i\end{array}\right.\text{ (21)}$$

Finally, the resulting combined deterioration-intervention matrix can be written as:

$${\overline{Q}}_C\left(x,i^{\text{'}}\right)={\overline{q}}_{ij}^{c,x}=\left\{\begin{array}{l}{\widehat{p}}_{ij}^1+{\overline{r}}_{ij}^{c,x}+{\overline{p}}_{in+1}^1\left[\delta {\widehat{r}}_{n+1j}^{1,x}+\left(1-\delta \right){\widehat{r}}_{n+1j-n}^{2,x}\right]{{\displaystyle }}_{}\forall i=1,2,\mathrm{...}n,j=1,\mathrm{2....}n+k\\ {\widehat{p}}_{ij}^2+{\overline{r}}_{n+ij}^{c,x}+{\overline{p}}_{in+1}^2\left[\delta {\widehat{r}}_{n+1j}^{1,x}+\left(1-\delta \right){\widehat{r}}_{n+1j-n}^{2,x}\right]{{\displaystyle }}_{}\forall i=1,2,\mathrm{...}k,j=1,\mathrm{2....}n+k\end{array}\right.\text{ (22)}$$

With:

$\left\{\begin{array}{l}{\widehat{p}}_{ij}^1={\overline{p}}_{ij}^1{{\displaystyle }}_{}\forall i\ne ì\text{'},i\le n,j\le n\\ {\widehat{p}}_{ij}^2={\overline{p}}_{ij}^2{{\displaystyle }}_{}\forall i\ne ì\text{'},i\ge n+1,j\ge n+1\\ {\widehat{p}}_{ij}^1=0{{\displaystyle }}_{}\forall j\ge n+1\\ {\widehat{p}}_{ij}^2=0{{\displaystyle }}_{}\forall j\le n\\ {\widehat{p}}_{ij}^1={\widehat{p}}_{ij}^2=0{{\displaystyle }}_{}\forall i=ì\text{'}\\ \delta =1{{\displaystyle }}_{}\forall j\le n\\ \delta =0{{\displaystyle }}_{}\forall j\ge n+1\end{array}\right.\text{ (23)}$

The CS of the element in any given year for interventions set x carried out on CSs ' i can be written as:

$${\Pi }_C\left(t,x,i^{\text{'}}\right)={\Pi }_C\left(0\right){\left({\overline{Q}}_C^{}\left(x,i^{\text{'}}\right)\right)}^t\text{ (24)}$$

Where

$${\Pi }_C\left(0\right)=\left\{\begin{array}{cccc}{\pi }_1^c\left(0\right)& {\pi }_2^c\left(0\right)& \cdots & {\pi }_{n+k}^c\left(0\right)\end{array}\right\}$$

is the CS distribution of the element at t = 0.

Similar to the previous section, the expected value of impacts in any given year can be written as:

$$\begin{array}{l}E\left(V_t\left(x,i^{\text{'}}\right)\right)={\displaystyle \sum _{\forall i=i^{\text{'}}\le n}^{}{\displaystyle \sum _{j=1}^n{\pi }_j^e\left(t-1\right){\overline{p}}_{ji}^1{\displaystyle \sum _{a=1}^A{c}_{a,x}^{e,I}}}}+{\displaystyle \sum _{\forall i=i^{\text{'}}\ge n+1}^{}{\displaystyle \sum _{j=1}^k{\pi }_{j+n}^e\left(t-1\right){\overline{p}}_{ji-n}^2{\displaystyle \sum _{a=1}^A{c}_{a,x}^{e,I}}}}\\ +{\displaystyle \sum _{j=1}^n{\pi }_j^e\left(t-1\right){\overline{p}}_{jn+1}^1{\displaystyle \sum _{a=1}^A{c}_a^{e,f}}}+{\displaystyle \sum _{j=1}^k{\pi }_{j+n}^e\left(t-1\right){\overline{p}}_{jk+1}^2}{\displaystyle \sum _{a=1}^A{c}_a^{e,f}}+{\displaystyle \sum _{j=1}^{n+k}{\pi }_j^e\left(t\right){\displaystyle \sum _{a=1}^A{c}_{a,j}^{e,D}}}\left(1-\frac{d_t\left(x,i^{\text{'}}\right)}{d_{T,t}}\right)\text{ (25)}\end{array}$$

where π^e_j (t −1) is the probability of element being in CS j in time t – 1, c ^e,I_a,x is the value of impact a in carrying out intervention x in non-structural failure CS ' i on element e, c^e,f_a is the value of impact a in an event of the failure of element e, c ^e,D_a,jis the value of impact a when the element is in operation and in CS j, d_{T ,t} is the length of the time interval t in days, and (x,i) ' d_t is the number of days per time interval t structure is out of service due to interventions x, which can be calculated as:

$\begin{array}{l}{d}_t\left(x,i^{\text{'}}\right)={\displaystyle \sum _{\forall i=i^{\text{'}}\le n}^{}{\displaystyle \sum _{j=1}^n{\pi }_j^e\left(t-1\right){\overline{p}}_{ji}^1{d}_x^{e,I}}}+{\displaystyle \sum _{\forall i=i^{\text{'}}\ge n+1}^{}{\displaystyle \sum _{j=1}^k{\pi }_{j+n}^e\left(t-1\right){\overline{p}}_{ji-n}^{e2}{d}_x^{e,I}}}\\ +{\displaystyle \sum _{j=1}^n{\pi }_j^e\left(t-1\right){\overline{p}}_{jn+1}^1}{d}_{n+1}^{e,f}+{\displaystyle \sum _{j=1}^k{\pi }_{j+n}^e\left(t-1\right){\overline{p}}_{jk+1}^2}{d}_{k+1}^{e,f}\text{ (26)}\end{array}$

where d^e,I _xis the number of days when the element will be out of service for interventions x carried out on non-structural failure CS ' i , and d^e,f_(n+1) and d^e,f_k+1 are the number of days when the element will be out of service due to structural failure. Similar to previous section, the optimal intervention strategy can be found using Equation 12, by replacing E(V_t(x,i')) by Equation 25.

A simplified method to determine the optimal intervention strategy

The method described above can be used to determine the optimal intervention strategy, by determining the intervention strategy resulting in the minimum life-cycle impacts. However, as the impacts are calculated each year, the calculation procedure may become computationally demanding. An alternative to determine the optimal intervention strategy is proposed in this section using the steady state properties[14], as is now being done in many existing bridge management systems (e.g. [9]). Under stationary transition conditions, the steady state probability of being in each CS i, π i , when interventions x are performed on CSs ' i can be calculated by solving the following set of equations:

$\left\{\begin{array}{l}{\overline{\pi }}_i\left(x,i^{\text{'}}\right)={\displaystyle \sum _{j=1}^{n+k}{\overline{q}}_{ij}^{c,x}{\overline{\pi }}_j\left(x,i^{\text{'}}\right)}\\ {\displaystyle \sum _{i=1}^{n+k}{\overline{\pi }}_i\left(x,i^{\text{'}}\right)}=1\end{array}\right.\text{ (27)}$

Using the steady state probabilities, the optimal intervention strategy can be calculated as:

Example

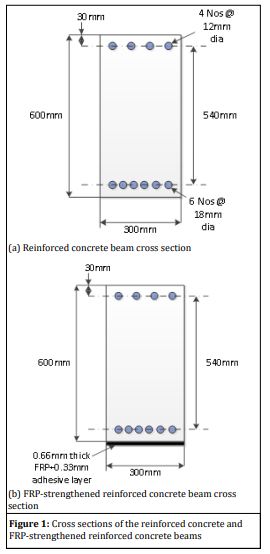
The purpose of this example is to demonstrate the use of the proposed methodology to determine the optimal intervention strategies for a hypothetical bridge element, when the interventions could change the deterioration rate. FRP strengthening of reinforced concrete (RC) bridge girders was assumed to be one of the available intervention options. For illustrative purposes, representatives RC beam cross sections with and without FRP strengthening are provided in Figure 1.

With FRP strengthening, extended life spans can be expected for bridge structures, thus the life-span of the bridge was taken as 150 years. Calculations were carried out using the methodology presented in Section 2 for each year. The intervention strategy resulting in the minimum total cost up to 150 years was taken as the optimal intervention strategy. Also, the optimal intervention strategy was determined based on the simplified method presented in Section 3. Details of the example are given in the following sections.

CS definitions

Typically, the CSs of RC elements subjected to reinforcement corrosion are defined in terms of reinforcement section loss [15].Similarly, in the current study the CSs for the RC beam were defined based on the reinforcement section loss (Table 1). As the main deterioration of the FRP strengthened RC beam is the bond degradation, the CSs for the FRP strengthened RC beam were defined using the bond strength loss (Table 1). The CSs of the RC beam are denoted by CCS, while the CSs of FRP strengthened RC beam are denoted by FCS. The CSs of the FRP strengthened RC beam were set so that, the worst CS (i.e. FCS3) gives equal performance to the worst CS for the RC beam (i.e.CCS5). The structural failure probabilities corresponding to each CS are also given in Table 1 for both RC beam and FRP strengthened RC beam. As this example is only to illustrate the methodology, details of the structural failure probability calculations are not discussed

Deterioration matrices

The transition probabilities of the deterioration matrix for the RC beam without considering the failure probabilities are given in Table 2. Time interval is taken as one year. These transition probabilities could be easily obtained using a stochastic corrosion model [16-17]. As the corrosion initiation starts only in CCS2, there is no change in annual structural failure probability from CCS1 to CCS2. From CCS2 to CCS5, annual structural failure probabilities increase due to strength loss as a result of reinforcement section loss. In CCS5, RC girder will be considered as unsafe due to its excessively high structural failure probability.

The transition probabilities of the adjusted deterioration matrix (Equations 3 and 4) considering annual structural failure probabilities are given in Table 3.

The transition probabilities of the deterioration matrix for the FRP strengthened RC beam, without considering the structural failure probabilities are given in Table 4. These transition probabilities could be estimated using an appropriate bond-degradation model coupled with a bond-strength model [18-19].

The transition probabilities of the adjusted deterioration matrix (Equations3 and 4) considering annual structural failure probabilities are given in Table 5.

Intervention options

The transition probabilities for different intervention activities are shown in Table 6. In this table the rows correspond to the bridge girder condition before the intervention is applied (at the beginning of the time interval where the intervention will be carried out), whereas the columns refer to the CS in the year following the intervention. Four possible interventions: concrete cover repair (possible in CCSs 2 and 3), concrete spalling and reinforcement repair (possible in CCSs 2 to 5), replacement with a new concrete beam (possible in CCSs 2 to 5, FCS3 and the structural failure CS, i.e. CSF), and FRP strengthening (possible in CCSs 2 to 5) were considered.

The identified intervention options are possible for bridge girders either alone or in various combinations. The possible intervention combinations are normally determined by an expert engineer. In many practical situations, the number of intervention types and combinations will be limited to a finite set. For this example a hypothetical list of possible intervention sets and the CSs in which each intervention is permitted are given in Table 7. In total, 5 different intervention sets with 20 possible intervention strategies result from the list given in Table 7.

The costs corresponding to the CSs and intervention actions are given in Table 8. They are divided into owner and public costs. These costs are hypothetical. However efforts were made to keep the ratios of their magnitudes reasonable. For the owner, cover repair is very cheap ($15,000), compared to spalling and reinforcement repair ($30,000), FRP strengthening ($35,000) or replacement ($60,000). Spalling and reinforcement repair is still cheaper than FRP strengthening, owing to the high material costs of FRP (even though FRP strengthening will have lower construction costs). For the public, costs during the interventions depend on the intervention action. The public costs considered here include costs due to noise during construction, increased travel costs due to construction work, environmental costs, etc. When the bridge is close, traffic has to be detoured and assumed to translate into an additional public cost of $500 per day. If the bridge girder experiences structural failure, a relatively high cost ($400,000) is used to represent the possible injury and reconstruction costs.

The public costs due to normal operations of the bridge were assumed to be dependent on the CS, and taken as $20,000,$2 4,000,$28,000,$35,000, and $80,000 for CCS 1-5 respectively and $20,000,$24,000, and $60,000 for FCS1-3 respectively. The relatively high public costs associated with CCS5 and FCS3 are due to disturbances to the normal operations (e.g. restricted load limits, etc.) owing to the reduced safety of the bridge. A simple Microsoft Excel spreadsheet was setup to do the calculations.

Results

The calculation of the costs up to 150 years for all intervention strategies was easily done using the spreadsheet. The calculation effort for the simplified method was significantly less than that for the year-by-year life cycle cost analysis up to 150 years. Both methods are believed to be much easier than the existing methods, which may require time-consuming MC simulations.

The calculated costs over 150 years and annual costs using stead state properties are given in Table 9 for all of the intervention strategies. In order to compare the results, normalized total costs, i.e. normalized with respect to the minimum cost for each method, are given in the last two columns. These normalized costs of each strategy are also plotted in Figure 2. It is obvious that the results from the simplified method generally are in a good agreement with the calculated results over 150 years. The small differences were found to occur due to differences in cost calculations in the years before reaching the steady state. For some intervention strategies, it was also found that the steady state properties are not yet achieved during the 150 years. The optimal strategy selected from the cost minimization over 150 years was set 3, with interventions for CCS2, CCS4, FCS3, and CSF, while the optimal strategy selected using steady state properties was set 2 with interventions for CCS2, CCS4, and CSF. However, the difference between the costs obtained using steady state properties of these two intervention strategies was only 0.2%. Considering generally good agreement of two methods (Figure 2), the simplified method can be taken as a good approximate method to determine the optimal intervention strategy.

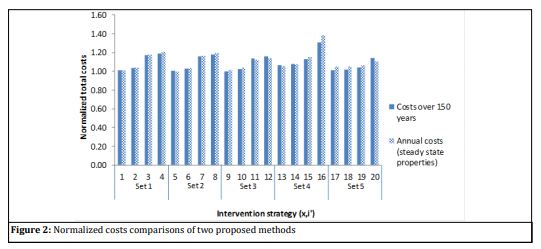
Table 1: CS description for reinforced concrete beams and FRP strengthened reinforced concrete beams

Table 2: Transition probability matrix for reinforced concrete beam

Table 3: Adjusted transition probability matrix for reinforced concrete beams

Table 4: Transition probability matrix for FRP strengthened beams

Table 5: Adjusted Transition probability matrix for FRP strengthened beams

Table 6: Intervention options and their effectiveness

Table 7: Possible intervention sets

Table 8: Bridge closure days and intervention costs

Table 9: The calculated costs up to 150 years and annual costs from steady state properties

Conclusions

This paper presents a methodology for evaluating the lifecycle impacts of intervention strategies for infrastructure such as bridges, which considers the possible changing deterioration rates due to interventions during the service life. The methodology was developed based on the Markovian approach commonly used in existing bridge management systems. The safety of the structure was also considered by introducing an additional condition state. Based on the steady state properties, a simplified method was proposed to determine the optimal intervention strategies.

The proposed methodology is demonstrated for a hypothetical concrete bridge girder, where one of the intervention options is FRP strengthening. Several intervention options resulting in 20 intervention strategies were compared. The optimal strategy was selected based on minimum total life-cycle cost up to 150 years as well as based on minimum annual costs determined using steady state probabilities.

The results showed that the proposed method can be effectively used to evaluate intervention strategies that result in deterioration rate changes, also in order to determine the optimal intervention strategies. Results from the simplified model show a good agreement with the results from the year-by-year life-cycle cost analysis. However, some discrepancies occurred due to steady state not yet being reached during the 150 year analysis period and/or due to differences in costs in the early years (before the steady state is reached). Nevertheless, the proposed methodology is seen to provide an efficient means of considering the effects of changing deterioration rates in evaluating the life-cycle impacts of intervention strategies.

References

1. Scherer WT, Glagola DM. Markovian models for bridge maintenance management. Journal of Transportation Engineering. 1994;120(1):37-51.
2. Roelfstra G. Modeled' evolution de l'etat des ponts-routes enbeton. These n°2310 – Grade de Docteurès Sciences Techniques, Doctoral Dissertation, ÉcolePolytechniqueFédéral de Lausanne. Switzerland (in French), 2001.
3. Orcesi A,Cremona C. Optimization of maintenance strategies for the management of the national bridge stock in France. Journal of Bridge Engineering, ASCE. 2011;16(1):44–52.
4. Almeida J, Teixeira P,Delgado R. Life cycle cost optimisation in highway concrete bridges management. Structure and Infrastructure Engineering. 2013;1-14.
5. Walbridge S, Fernando D, Adey BT. Cost-benefit analysis of alternative corrosion management strategies for a steel roadway bridge.Journal of Bridge Engineering,ASCE. 2013;18(4):318-327.
6. Fernando D, Mirazei Z, Adey BT, Ellis RM. The application of benefit hierarchy to determine the optimal intervention strategies for bridges. Transportation Research Board 91st Annual Meeting. 2012:22-26, Washington D.C.
7. Thompson PD, Small EP, Johnson M, Marshall AR. The Pontis bridge management system. Structural Engineering International, IABSE. 1998;8:303-308.
8. Pontis. Version 4.0 Technical Manual Report. USA: FHWA, US Department of Transportation. USA, 2001.
9. KUBA. KUBA-MS-Ticino-user's manual, release 3.0., F.D.o. Highways, Bern, Switzerland, 2005.
10. Jiang Y, Sinha KC. Bridge service life prediction model using markov chain. Transportation Research Record. 1989;1223:24-30.
11. Toutanji H, Gomez W. Durability characteristics of concrete beams externally bonded with FRP composite sheets. Cement and Concrete Composites. 1997;19:351-358.
12. Karbhari VM, Chin JW, Hunston D, Benmokrane B, Juska T, Morgan R, Lesko JJ, Sorathia U, Reynaud D. Durability gap analysis for fiber-reinforced polymer composites in civil infrastructure. Journal of Composites for Construction, ASCE. 2003;7 (3):238-247.
13. Robelin CA, Madanat S. History-dependent bridge deck maintenance and replacement optimization with Markov decision processes, Journal of Infrastructure Systems, ASCE. 2007;13(3):195-201.
14. Ching WK, Huang X, Ng MK, Siu TK. Markov chains: models, algorithms and applications.International series in operations research & management science. Springer Science Business Media. 2013;189: New York, USA.
15. Pontis. Pontis Bridge Inspection Manual. M.D.o. Transportation, Michigan, USA, 2007.
16. Pedersen C, Thoft-Christensen P. Reliability analysis of prestressed concrete beams with corroded tendons.Instituttet for Bygningsteknik, Aalborg Universitetscenter, 1993.
17. Vu KAT, Stewart MG. Structural reliability of concrete bridges including improved chloride-induced corrosion models. Structural Safety. 2000;22:313-333.
18. Ouyang Z, Wan B. Modeling of moisture diffusion in FRP strengthened concrete specimens. Journal of Composites for Construction, ASCE. 2008;12(4):425-434.
19. Tuakta C, Büyüköztürk O. Conceptual model for prediction of FRP-concrete bond strength under moisture cycles. Journal of Composites for Construction, ASCE. 2011;15(5):743-756.